Introduction to Critical Fallibilism

Critical Fallibilism (CF) is a philosophical system that focuses on dealing with ideas. It has concepts and methods related to thinking, learning, discussing, debating, making decisions and evaluating ideas. CF combines new concepts with prior knowledge. It was created by me, Elliot Temple.

(If you'd prefer to watch a summary video before reading this article, click here.)

From Critical Rationalism (CR), by Karl Popper, CF accepts that we’re fallible (we often make mistakes and we can’t get a guarantee that an idea is true) and we learn by critical discussion. Learning is an evolutionary process which focuses on error correction, not positive justification for ideas. We can’t establish that we’re right (or probably right), but we can make progress by finding and correcting errors. Positive arguments and induction are errors.

From Theory of Constraints (TOC), by Eli Goldratt, CF accepts focusing on constraints (bottlenecks, limiting factors) for achieving goals. Most factors have excess capacity and should not be optimized. Optimizing them is focusing on local optima (trying to improve any factor) instead of global optima (considering which improvements will make a significant difference to a big picture goal, and focusing on those). Optimization away from the constraint is wasted. TOC also explains using tree diagrams, using buffers to deal with variance, and finding silver bullet solutions using inherent simplicity.

From Objectivism, by Ayn Rand, CF accepts that learning involves integration and automatization. We can only actively think about a few ideas at once (roughly seven). To deal with complex or advanced ideas, we must integrate (combine) multiple simpler ideas into a single conceptual unit – a higher level idea. We can do this in many layers to build up to advanced ideas. Like integration, automatization also helps fit more in our mind at once. It involves practicing to make things automatic (habitual, intuitive, second-nature, mastered) so they require little or no conscious attention. Automatization works with physical actions (like walking) and with mental actions (like recognizing decisive arguments).

CF also accepts that digital systems are fundamentally better at error correction than analog systems. This comes from computer science theory and is a reason that modern computers are digital.

CF builds on these ideas and combines them into a single philosophy along with some new ideas.

Decisive Arguments

CF’s most important original idea is the rejection of strong and weak arguments. CF says all ideas should be evaluated in a digital (specifically binary) way as non-refuted (has no known errors) or refuted (has a known error). Binary means there are two possibilities. An error is a reason that an idea fails at a goal. We shouldn’t evaluate ideas by how good they are (by their degree or amount of goodness); instead we should use pass/fail evaluations. This idea was initially developed when trying to clarify and improve on CR.

There are many terms people use to discuss how good ideas are, including credence, validation, justification, support, plausibility, certainty, truthlikeness, probability, strength, weight, power, corroboration, verisimilitude, confidence level and degree of belief.

CF says valid arguments are criticisms or equivalent to criticisms. A criticism should contradict an idea and explain that the idea fails. Criticisms should be decisive, rather than merely saying an idea isn't great. That means you don't accept both the criticism and its target because they’re incompatible (unless you find an error in some background knowledge, e.g. a flaw in your understanding of logic that affects whether they contradict).

All ideas, including criticisms we accept, are held tentatively. That’s a CR idea which means we know we’re fallible and might have to revise our views in the future when we think of new ideas or get new evidence. We can reach conclusions and even be confident, but we simultaneously expect that we don’t have the perfect, final truth. Believing there is a possibility for further improvements or progress doesn't require us to be indecisive, uncertain, hesitating people who struggle to make a decision or take action.

Note that the idea CF rejects is not about numbers. The problem with degrees or amounts of goodness is present whether you try to numerically quantify them or not. In his book Objectivism: The Philosophy of Ayn Rand, Leonard Peikoff evaluates ideas as arbitrary, possible, probable or certain. He says ideas gain validation, and can improve to the next status, as we accumulate evidence. That non-numeric approach is about judging how good ideas are, so CF rejects it.

If all ideas have only two evaluations (refuted or non-refuted), how can we differentiate which ideas are better or worse? In other words, CF rejects giving an idea a score (or credence, probability, confidence, degree of belief, etc.) like 80 out of 100. But I’m more confident in some ideas that I accept than others. If CF can only score ideas as exactly 0 or 1, how can it express a difference between two good ideas that both score a 1?

CF’s alternative to degrees of confidence or goodness for ideas is giving ideas multiple evaluations. Ideas can be differentiated, even though they receive the same score in some cases, because they receive different scores in other cases. Instead of trying to fit complexity or nuance into a single score or non-numeric evaluation, CF gives ideas many evaluations but keeps each evaluation simple. Having multiple simple things, instead of one more complicated thing, is a different way to get complexity or nuance.

What things do you evaluate ideas for? Different purposes/goals. An idea can be good for one purpose and bad at another purpose. For example, the idea “use a hammer” works for the goal of nailing wood together but fails for the goal of serving soup. Context matters too: a combat plan could succeed for soldiers fighting in a forest but fail in a desert.

CF says that to differentiate two rival ideas, and say one is better than the other, you must identify at least one goal for which one idea is non-refuted and the other is refuted. Rival ideas are ideas that make contradictory claims about the same issue. They’re alternatives or competitors. Because they contradict, we should choose at most one of them. Non-rival ideas don’t need to be compared to each other because they’re compatible.

To say one idea is better than another, you must be able to point out what goal it succeeds at which the other fails at. The goal you use to differentiate two ideas should also be relevant and important, e.g. use a goal that you actually have in your life.

Ideas should not be evaluated in isolation, out of context. Instead of evaluating ideas alone, think of evaluating (idea, goal) pairs. You can also specify the context explicitly and evaluate (idea, goal, context) triples (called IGCs). Every pair or triple should be evaluated as either refuted or non-refuted: do we know of a decisive error or not? If we evaluate multiple IGCs containing an idea, then we have multiple evaluations related to that idea.

A decisive error is a reason an idea fails at a goal. A non-decisive error is compatible with success and is therefore not really an error. We should look for decisive errors; they’re what refute ideas (for goals).

What if several criticisms each individually don’t refute an idea, but their combination does? Can indecisive criticisms add up to a decisive criticism? Yes, sometimes. E.g. a plan may work despite X happening, or despite Y happening, but fail if both X and Y happen. In that case, form a new, larger criticism that combines the smaller criticisms. The decisive criticism would explain both X and Y, say why both will happen, and say how that will lead to failure. Although none of the original criticisms (about X or Y alone) were decisive, the new criticism is.

Once we think in terms of evaluating ideas for many goals, we encounter a difficulty. There are infinitely many logically-possible goals. So how do we choose goals to consider? We have to make choices about what we want. It’s up to us to decide what we value. We can use some common, generic goals like being happy, healthy, wealthy, peaceful, kind and honest. We can have a goal to figure out what’s true. We can use field-specific goals, e.g. when doing a math problem we’d want to get an answer that is correct according to the rules of arithmetic. If we find these goals unsatisfactory we can search for better goals and better ways of judging goals.

There are also infinitely many possible ideas and contexts. How do we deal with that? Rather than evaluating all ideas or random ideas, evaluate ideas that you think might be good. We commonly also evaluate ideas that other people think might be good. Regarding context, we frequently evaluate using our own current context. Sometimes we consider a predicted future context where a few things are different. And sometimes we evaluate a different context, e.g. if you’re giving someone advice you should consider their context instead of your own.

This limits the number of ideas, goals and contexts that we evaluate. That keeps the number of IGCs to evaluate more manageable.

Note that CF does not reject statistics or probabilities in general, which are useful tools. Evidence, and the statistical properties of that evidence, can be seen as inputs which are used by a binary thinking process that judges ideas. Ideas should be judged with critical arguments that take into account and refer to data and statistics, not directly by data or statistics (which are most similar to facts, not to evaluations, conceptual analysis, explanations or reasoning).

Binary Goals

CF uses binary goals. Well-defined, binary goals unambiguously define success and failure. Whatever the outcome, there is a correct answer about whether it was success or failure (even if you don't know the answer). There is no partial success. This works like binary logic: well-defined propositions are true or false, never partially true.

It's fine to say that a statement of a goal is ambiguous, or to say that you don't know something. Neither of those is a claim about partial success. Also, claims of ignorance or ambiguity are reasons for not evaluating something rather than alternative evaluations besides success or failure.

The main proposal for non-binary goals is degrees of success. Can two plans both succeed, but one succeeds more? If that worked, it'd be an alternative to CF. But goals using degrees of success are usually vaguely-stated binary maximization goals (so not really a non-binary approach). Also, we usually shouldn't try to maximize.

For example, suppose the degrees of success are the amount of money you get. You say that anything over $100 is success, and $300 is better (more success) than $200. This is an unclear way of stating a maximization goal because it's treating money in a "the more, the better" way, which means money should be maximized. Everything else being equal, choosing a plan that gets you $200 is an error when another plan would get you $300.

Since we're maximizing money, that creates a binary distinction between plan(s) that give the maximum amount of money (success) and plans that give less (failure). There aren't really degrees of success here because any amount of money less than the maximum is, everything else being equal, simply a failure: there's no reason to pick it and picking it is an error.

Everything else usually isn't equal, so single-factor maximization is usually unwise and people rarely try to do it. But using multiple factors runs into major difficulties and is still focused on maximization.

More generally, any complete, correct formula that defines amounts of success based on any number of factors suggests that you should maximize success (which brings us back to binary goals). If maximizing the formula doesn't give you the best outcome, that means the formula is incomplete or wrong. If it's imperfect but a good enough approximation to use, that suggests maximizing it. There's no reason to choose not-best over best unless your way of evaluating is incomplete or wrong (so we end up with binary evaluations: best = success and not-best = failure).

So looking at degrees of success approaches more closely leads to finding that they're misleading ways to express binary maximization goals or they're incomplete or wrong.

Also, maximizing degrees or amounts of one or more factors is usually not what we should do. Even if we convert a vague degrees-of-success goal to a precise binary maximization goal, it's usually a bad goal.

Good goals typically aim for enough of one or more factors (including a margin of error), not to maximize them. This creates a binary distinction between enough and not enough.

Most factors are not bottlenecks, and already have excess capacity, so we shouldn't be trying to maximize them because we already have enough. Increases in excess capacity can be mildly bad because they e.g. take up additional storage space or distract us from more important issues. But as a first approximation, which is usually good enough, small or medium sized changes in excess capacity simply don't matter. So instead of trying to maximize how much we get of various factors, we should recognize that a bit more or less of most factors is irrelevant.

Most differences in quantities aren’t important, which helpfully reduces the burden on our limited time and attention. We don’t need to take into account most information or factors at all, which is good because reality is vastly complex. For things we do take into account, almost all of them should be evaluated in a pass/fail way based on whether they cause a major problem or not. As long as there is no major problem, they pass, and we don’t analyze them further. (E.g. we check that we do have excess capacity, not a shortage, and that's all the attention many factors get. We're just checking that they're good enough.)

There’s so much stuff in reality, and in all logically possible ideas we could have, that we can never hope to consider much of it. We have to focus on important issues, which we should divide into two main categories. Most issues we analyze should receive a quick pass/fail evaluation (and if any fail, we either reject the idea or give the failure more attention). For the few things we give more attention and nuance to, CF says to use multiple binary evaluations rather than one (or multiple) non-binary evaluations.

Breakpoints

We can broadly look at things as either small digital or analog. “Small digital” means something is digital with a small number of possible values. For example, it could be binary, there could be four discrete categories, or it could have a whole-numbered value from 1 to 5. Analog means spectrums, continuums, quantities, amounts, degrees or real numbers. Large digital (e.g. the integers from one to a thousand, or to infinity) might seem like a third category, but we can usually treat it like analog; for most purposes, large digital approximates to analog.

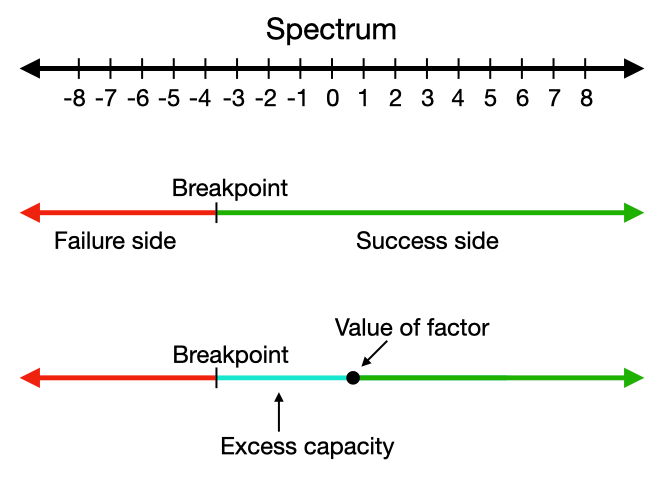
A breakpoint is a point on an analog spectrum where there’s a qualitative difference rather than merely a quantitative difference. (By definition, every point on a spectrum is slightly quantitatively different than the adjacent points.) Breakpoints split an analog spectrum into discrete categories. By using breakpoints, we can deal with everything in small digital terms. And each individual breakpoint can be dealt with in a binary way: there are two sides of a breakpoint, and a value falls on one of those two sides.

Most small changes in quantities don’t really matter because they don’t result in crossing a breakpoint. Breakpoints are very rare compared to non-breakpoints. Even many medium or large changes in quantities don't cross a breakpoint. If a change affects success or failure at your goal, that’s a qualitative difference and there’s a breakpoint there. If no breakpoint is crossed, then a change doesn’t change failure to success (or vice versa). Excess capacity is the amount of a factor that's far from any breakpoint so it doesn't help cross any breakpoint.

Goals for quantities are about being on a certain side of a breakpoint (in order to get a certain category of outcome). That makes the goal binary: success is doing better than the breakpoint and failure is doing worse than the breakpoint. The breakpoint is usually about “good enough” not maximization.

Goals can also be about qualitative differences that don't involve quantities, analog spectrums or breakpoints. The taste of an orange isn’t just a larger or smaller quantity of the taste of an apple. It’s a different type of taste. With quantities, we use breakpoints to turn an analog spectrum into categories. In other cases, we already have separate categories, so we don't need breakpoints and just have to determine which categories satisfy our goal and which don’t. This provides a binary distinction between satisfactory and unsatisfactory categories.

Broadly, it’s important to recognize that most factors have a large amount of excess capacity. They are more than good enough to succeed at our goal(s). We don’t need to increase most factors, and options with a bit less excess are not worse. We shouldn’t be looking to get the most of everything. Instead, we should be identifying at most a few key factors and only optimizing those. We need to focus our limited energy and attention where they'll have a large impact, and we need to recognize that more of a good thing isn't always better, not even a little bit better. The value we get from factors is typically non-linear, with large areas with little or no change and one or more small areas of rapid change. People tend to intuitively assume that more of a good thing is linearly better, which is false and leads to errors when evaluating ideas and to worse decision making.

Conclusion

Critical Fallibilism (CF) is an ambitious philosophy aiming at large progress and reform, but it also respects some tradition and existing knowledge. It builds on prior ideas like Critical Rationalism, Theory of Constraints, and Objectivism, as well as some parts of math, logic, grammar and common sense.

This article introduced ideas about binary thinking. But CF isn’t just an abstract philosophy. It also has specific methods (not covered in this article) that you can use to evaluate ideas or IGCs, find breakpoints, choose between goals, make decisions, solve problems and more.

To summarize binary thinking, you can evaluate ideas by considering a series of yes-or-no questions, some of which will relate to breakpoints. This has a variety of advantages; it's a nice system. Also, CF has arguments (not covered in this article) that alternative thinking methods run into logical problems and don't work.

CF also covers other topics related to rationality. It explains learning with practice to achieve mastery. It explains resource budgeting including viewing error correction capacity as a resource. And it explains a way to organize ideas and debate, over time, to reach conclusions. One idea is: If you’re mistaken, and someone else knows about the error and is willing to share their criticism, is there a good way for you to be corrected? Or are there issues (like ignoring unpopular ideas) that may lead to you staying wrong?

Overall, CF helps explain how reasoning works. It provides tools and methods you can use to think better. It’s more about how to think than what to think. It enables you to think better rather than telling you what beliefs to have. Even if you master CF, you’ll still have to think for yourself. This is like how the scientific method and pro/con lists are useful tools to help improve your thinking but they still leave you to think for yourself with no guarantee of a correct answer.

If you’re interested in learning more about CF, sign up to receive emails and read more articles. There are also CF videos and a discussion forum.

This article also has a companion video: